2ª Atividade de Linguagem Matemática, Ciências da natureza e suas tecnologias.

CIÊNCIAS:

INTRODUÇÃO A ONDULATÓRIA

A PROPAGAÇÃO DO SOM E O OUVIDO HUMANO

ATIVIDADES:

1. Quando, em uma região plana e distante de obstáculos, se ouve o som de um avião voando, parece que esse som vem de uma direção diferente daquela em que, no mesmo instante, se enxerga o avião. Considerando-se essa situação, é CORRETO afi rmar que isso ocorre porque:

A) a velocidade do avião é maior que a velocidade do som no ar.

B) a velocidade do avião é menor que a velocidade do som no ar.

C) a velocidade do som é menor que a velocidade da luz no ar.

D) o som é uma onda longitudinal e a luz uma onda transversal.

E)    Nda.

2, Os morcegos, quando voam, emitem ultrassom para que, através das reflexões ocorridas pelos obstáculos à sua frente, possam desviar deles, e também utilizam esse mecanismo para se orientarem durante seu vôo. Imagine um morcego voando em linha reta horizontal com velocidade V, em direção a uma parede vertical fixa. Considere que não esteja ventando e que a fonte sonora no morcego seja puntiforme e então, quando ele ainda está a uma certa distância da parede, emite uma onda sonora com uma frequência f de ultrassom. Com fundamentos da mecânica ondulatória, assinale a(s) proposição(ões) correta(s).

A) A velocidade das ondas sonoras que possuem frequência de ultrassom é maior que a velocidade de ondas sonoras que possuem frequência menor que as de ultrassom.

B) A velocidade da onda sonora no ar, emitida pelo morcego em movimento, é diferente da velocidade da onda sonora no ar emitida pelo morcego quando em repouso.

C) A frequência da onda sonora, refletida pela parede e percebida pelo morcego, é maior que a frequência da onda sonora emitida por ele.

D) A velocidade da onda sonora no ar, refletida pela parede, é igual à velocidade da onda sonora no ar emitida pelo morcego.

E) Esse efeito de mudança na frequência de ondas sonoras emitidas por fontes em movimento chama-se batimento.

3. Independentemente da natureza de uma onda, sua propagação envolve, necessariamente:  

      a) movimento de matéria;

      b) transporte de energia;

      c) transformação de energia;

      d) produção de energia;

      e) transporte de energia e de matéria.   

4, Quais as características das ondas sonoras que determinam a altura e a

intensidade do som?

a) comprimento de onda e freqüência

b) amplitude e comprimento de onda

c) amplitude e freqüência

d) freqüência e comprimento de onda

e) freqüência e amplitude

5. O som não se propaga no vácuo porque:  

      a) é uma onda longitudinal;

      b) é uma onda mecânica;

      c) não é tridimensional;

      d) é uma onda eletromagnética;

      e) não é uma onda estacionária. 

6. Uma pessoa toca no piano uma tecla correspondente à nota mi e, em seguida, a 

que corresponde a sol. Pode-se afirmar que serão ouvidos dois sons diferentes porque as 

ondas sonoras correspondentes a essas notas têm:

a) amplitudes diferentes

b) freqüências diferentes

c) intensidades diferentes

d) timbres diferentes

e) velocidade de propagação diferentes

6. Som mais agudo é som de:

a) maior intensidade

b) menor intensidade

c) menor freqüência

d) maior freqüência

e) maior velocidade de propagação

7.  Quando uma onda sonora se propaga no ar, numa certa direção:  

 a) o ar, como um todo, se desloca na direção da propagação da onda;

 b) o ar, como um todo, se desloca na direção normal à direção de propagação da onda;

 c) as partículas do ar se movimentam de um lado para outro, numa direção normal à direção da propagação da onda;

 d) as partículas do ar se movimentam para frente e para trás, na direção da propagação da onda;

 e) o ar não se movimenta, apenas sua pressão aumenta e diminui sucessivamente.   

8.  Um caçador ouve o eco de um tiro 6,os após ter disparado a arma. Sabendo-se que o som se propaga no ar com velocidade de módulo igual a 340m/s, o anteparo refletor encontra-se a uma distância igual a:  

      a) 2 040m

      b) 1 020m

      c) 510m

      d) 340m

      e) 680m   

9. Som mais agudo é som de:

a) maior intensidade

b) menor intensidade

c) menor freqüência

d) maior freqüência

e) maior velocidade de propagação

10. Complete os trechos relacionando corretamente as palavras abaixo:

eletromagnéticas - transversais - 300000 m/s - mecânicas - longitudinais - mistas.

a) As ondas luminosas quanto à sua natureza são _______________ pois se propagam no 

vácuo; quanto à direção de propagação e vibração são ________________ e se 

propagam no vácuo com velocidade igual a ____________________.

b) As ondas sonoras quanto à natureza são _________________ pois não se propagam 

no vácuo; quanto à direção de propagação e vibração são ____________________ nos 

fluidos e ______________________ nos sólidos.

MATEMÁTICA:

VELOCIDADE E ACELERAÇÃO.

Velocidade Média

Aceleração média

ATIVIDADES:

1. Um móvel percorre uma distancia de 1200 m em 4 min. Qual a sua velocidade escalar media em m/s?

2. Uma partícula percorre 30 m com velocidade escalar media de 36 km/h. Em quanto tempo faz este percurso?

3.Se um veículo passa sua velocidade de 2 m/s para 12 m/s em 2 s, qual sua aceleração escalar

média?

4. Uma partícula parte do repouso e em 5 segundos percorre 100 metros. Considerando o movimento retilíneo e uniformemente variado, podemos afirmar que a aceleração da partícula é de:

a) 8 m/s2

b) 4 m/s2

c) 20 m/s2

d) 4,5 m/s2

e) Nenhuma das anteriores

TRABALHO E ENERGIA.

Uma força somente realiza Trabalho se houver deslocamento do corpo no qual ela atua. Dessa forma, se uma pessoa em repouso segura um objeto, ela não está realizando Trabalho. Analisando dessa forma podemos relacionar esses acontecimentos com a seguinte equação matemática para o Trabalho realizado por uma força:  , onde τ (letra grega tau) = trabalho, F = força e d = deslocamento.

Em algumas situações o trabalho é realizado de forma mais rápida. Por exemplo, um percurso de uma maratona foi realizado por duas pessoas em tempos diferentes. Nesse caso dizemos que a pessoa que realizou o percurso em menos tempo desenvolveu uma maior potência média em relação a outra. Com base nessa definição temos que a equação matemática responsável pelo cálculo da potência de um corpo é dada pela expressão: , onde ∆t: variação de tempo.

                                                                       ATIVIDADES

QUESTÃO 1: Determine o trabalho realizado por uma Força de intensidade 250 N (Newton) aplicada sobre um corpo, o qual se desloca por 20 metros no mesmo sentido da força.

QUESTÃO 2: Uma força de intensidade 40 N é aplicada a um corpo, deslocando-o por 5 metros na direção e sentido da força, durante 10 segundos. Com base nessas informações calcule:

a) o trabalho realizado pela força.
b) a potência média dessa força.

Energia Cinética, Potencial e Mecânica

De um modo geral, a energia pode ser definida como capacidade de realizar trabalho ou como o resultado da realização de um trabalho. Na prática, a energia pode ser melhor entendida do que definida. Quando se olha para o Sol, tem-se a sensação de que ele é dotado de muita energia, devido à luz e ao calor que emite constantemente.

  

Uso da Energia

A humanidade tem procurado usar a energia que a cerca e a energia do próprio corpo, para obter maior conforto, melhores condições de vida, maior facilidade de trabalho, etc.

Para a fabricação de um carro, de um caminhão, de uma geladeira ou de uma bicicleta, é preciso Ter disponível muita energia elétrica, térmica e mecânica.

A energia elétrica é muito importante para as indústrias, porque torna possível a iluminação dos locais de trabalho, o acionamento de motores, equipamentos e instrumentos de medição.

Para todas as pessoas, entre outras aplicações, serve para iluminar as ruas e as casas, para fazer funcionar os aparelhos de televisão, os eletrodomésticos e os elevadores. Por todos esses motivos, é interessante converter outras formas de energia em energia elétrica.

Energia Mecânica

Chamamos de Energia Mecânica a todas as formas de energia relacionadas com o movimento de corpos ou com a capacidade de colocá-los em movimento ou deformá-los.

Energia Cinética

A energia que um corpo adquire quando está em movimento chama-se energia cinética. A energia cinética depende de dois fatores: da massa e da velocidade do corpo em movimento.

Qualquer corpo que possuir velocidade terá energia cinética. A equação matemática que a expressa é:

QUESTÃO 3: Uma bala de revolver, de 0,10kg de massa, atinge uma velocidade de 10 m/s. Calcule a energia cinética da bala quando atinge essa velocidade.

QUESTÃO 4: Qual a energia cinética de um carro com massa 1500 kg que viaja a 20 m/s?

Energia Potencial

É um tipo de energia que o corpo armazena, quando está a uma certa distância de um referencial de atração gravitacional ou associado a uma mola.

Existe uma forma de energia que está associada a posição, ou melhor, uma energia que fica armazenada, pronta para se manifestar quando exigida, esta forma de energia recebe o nome de Potencial.

Quando discutimos o conceito de trabalho, falamos sobre dois casos especiais: o trabalho do peso e da força elástica. Esses trabalhos independem da trajetória e conduzem ao conceito de uma nova forma de energia – Energia Potencial.

♦ Energia Potencial  Gravitacional (E_PG)

Devido ao campo gravitacional um corpo nas proximidades da superfície terrestre tende a cair em direção ao centro da Terra, este movimento é possível devido a energia guardada que ele possuía. Esta energia é chamada Potencial Gravitacional.

Para Calcular: E_pg = m . g . h

QUESTÃO 5: Um corpo com massa de 2 kg está a uma altura de 160 m do solo. Calcular a energia potencial gravitacional desse corpo em relação ao solo, considerando g=10 m/s2.

QUESTÃO 6: Determine a energia potencial gravitacional, em relação ao solo, de uma jarra com água, de massa 2 kg, que está sobre uma mesa de 0,80 m de altura, num local onde g=10 m/s2.

♦ Energia Potencial  Elástica (E_PE)

Ao esticarmos ou comprimirmos uma mola ou um elástico, sabemos que quando soltarmos esta mola ela tenderá a retornar a sua posição natural (original). Essa tendência de retornar a posição natural é devido a algo que fica armazenado na mola a medida que ela é esticada ou comprimida. Este algo é a energia potencial elástica.

Para Calcular: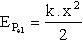 

QUESTÃO 7: Uma mola é deslocada 0,10 m da sua posição de equilíbrio; sendo a constante elástica desta mola equivalente à 50 N/m, determine a energia potencial elástica associada a esta mola em razão desta deformação.

MATEMÁTICA APLICADA:

PORCENTAGEM

 JUROS

ATIVIDADES:

01. Numa cidade de 50000 habitantes, 42000 têm menos de 40 anos de idade. Qual é a porcentagem dos que têm 40 anos ou mais?

02. Quais são os juros simples produzidos por um capital de R$ 7200,00 empregados a 10% ao ano, durante 5 anos?

03. A que taxa anual foi empregado o capital de R$ 108.000,00 que, em 130 dias, rendeu juros simples de R$ 3.900,00?

04. Em uma promoção numa revenda da carros, está sendo dado um desconto de 18% para pagamento à vista. Se um carro é anunciado por R$ 16.000,00, então o preço para pagamento à vista desse carro será:


a) R$ 13.120,00

b) R$ 13.220,00

c) R$ 13.320,00

d) R$ 13.420,00

e) R$ 13.520,00

PROBABILIDADE:

ATIVIDADES:

1. Na lista de chamada de uma turma, os 30 alunos são numerados de 1 a 30. Em certo dia, quando faltaram os alunos de 11 e 26, o professor sorteou um aluno para resolver umas atividades no quadro. Qual é a probabilidade do número sorteado ser:

a) Par?

b) Menor que 9?

c) Múltiplo de 4?

d) Primo?

e) Maior que 12 e menor que 25?

2. Considere todos os números de 3 algarismos distintos formados com os algarismos 6,7 e8. Se escolhermos um desses números ao acaso. Calcule a probabilidade de ele ser:

a) Ímpar?

b) Par

c) Múltiplo de 3?

d) Múltiplo de 5?

MEDIA ARITMÉTICA:

ATIVIDADES:

1) Calcule a média aritmética simples em cada um dos seguintes casos:

a) 15 ; 48 ; 36

b) 80 ; 71 ; 95 ; 100

c) 59 ; 84 ; 37 ; 62 ; 10

2) 

O dólar é considerado uma moeda de troca internacional, por isso o seu valor diário possui variações. Acompanhando a variação de preços do dólar em reais durante uma semana verificou-se as variações de acordo com a tabela informativa:

Segunda	Terça	Quarta	Quinta	Sexta
R$ 2,30	R$ 2,10	R$ 2,60	R$ 2,20	R$ 2,00

Determine o valor médio do preço do dólar nesta semana. 

3) Em uma empresa existem cinco faixas salariais divididas de acordo com a tabela a seguir: 

Grupos	Sálario
A	R$ 1.500,00
B	R$ 1.200,00
C	R$ 1.000,00
D	R$ 800,00
E	R$ 500,00

Determine a média de salários da empresa. 

4) João deseja calcular a média das notas que tirou em cada uma das quatro matérias a seguir. Calcule a média ponderada de suas notas, sendo que as duas primeiras provas valem 2 pontos e as outras duas valem 3 pontos:

Matemática
1ª prova	8,5
2ª prova	9,2
3ª prova	9,6
4ª prova	10,0

MEDIA E DESVIO PADRÃO:

Os estudos estatísticos referentes ao Ensino Fundamental abordam os temas ligados à moda, mediana e média aritmética na análise de dados em geral. Esses termos são responsáveis por uma análise superficial dos dados coletados. Caso seja necessário um diagnóstico mais complexo da situação, devemos utilizar a metodologia do Desvio Padrão.

Os conceitos teóricos envolvendo o Desvio Padrão somente serão trabalhados no Ensino Médio. A melhor metodologia na abordagem desse conteúdo envolve a análise de dados de uma determinada situação distribuídos em tabelas. Vamos apresentar uma sequência de estudos voltados para a melhor compreensão do conceito e aplicação do Desvio Padrão.

Um curso pré–vestibular é composto de duas salas com 15 alunos cada. O diretor desse curso necessita saber qual das turmas possui o melhor rendimento geral. Para isso criou as seguintes tabelas com a média anual das notas obtidas nos simulados realizados pelos alunos durante o ano vigente. Observe as tabelas:

A média aritmética das notas é calculada através da divisão entre o somatório das notas e o número de alunos. Observe que, pela média aritmética, não podemos determinar qual sala obteve o melhor aproveitamento, pois as médias foram idênticas. Para visualizar qual a turma com a melhor regularidade de notas será necessário calcular o Desvio Padrão. Veja o método para esse cálculo:

Vamos subtrair cada nota individual da média aritmética:

Alguns resultados obtidos possuem o sinal negativo, vamos elevar todos os valores da diferença ao quadrado, constituindo os valores chamados de variância. Veja:

A razão entre o somatório dos valores da variância e o número de alunos constitui a média da variância. O Desvio Padrão será calculado através da raiz quadrada dessa média. Observe:
Desvio Padrão da sala 1

DP = √2,8
DP = 1,67

Desvio Padrão da sala 2

DP = √0,76
DP = 0,87

Os resultados indicam que a sala 1 obtém notas 1,67 acima ou abaixo da média e a sala 2 notas 0,87 acima ou abaixo da média. Mostre aos alunos que a sala 2 possui alunos mais homogêneos, enquanto a sala 1 possui alunos mais heterogêneos.

ATIVIDADES:

1. Qual a importância do desvio padrão na analise de dados de uma pesquisa?

2. Certamente você já ouviu algo sobre a margem de erros de uma pesquisa eleitoral. Você consegue identificar alguma relação da mesma com o desvio padrão?