1ª Atividade de Matemática e suas aplicações no Ensino Médio - Conjuntos Numéricos.

Conjuntos Numéricos

· Conjunto dos Números Naturais (IN)

Um subconjunto importante de IN é o conjuntoIN*:

IN*={1, 2, 3, 4, 5,...} ► o zero foi excluído do conjunto IN.

Podemos considerar o conjunto dos números naturais ordenados sobre uma reta, como mostra o gráfico abaixo:

· Conjunto dos números inteiros (Z)

O conjunto IN é subconjunto de Z.

Temos também outros subconjuntos de Z:

Z* = Z-{0}

Z₊ = conjunto dos inteiros não negativos = {0,1,2,3,4,5,...}

Z_ = conjunto dos inteiros não positivos = {0,-1,-2,-3,-4,-5,...}

Observe que Z₊ = IN.

Podemos considerar os números inteiros ordenados sobre uma reta, conforme mostra o gráfico abaixo:

· Conjunto dos números racionais (Q)

Os números racionais são todos aqueles que podem ser colocados na forma de fração (com o numerador e denominador 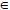 Z). Ou seja, o conjunto dos números racionais é a união do conjunto dos números inteiros com as frações positivas e negativas.

Então: 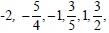 por exemplo, são números racionais.

Exemplos:

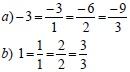
Assim, podemos escrever:

É interessante considerar a representação decimal de um número racional 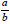, que se obtém dividindo a por b.

Exemplos referentes às decimais exatas ou finitas.

Exemplos referentes às decimais periódicas ou infinitas:

Toda decimal exata ou periódica pode ser representada na forma de número racional. 

· Conjunto dos números irracionais 

Os números irracionais são decimais infinitas não periódicas, ou seja, os números que não podem ser escrito na forma de fração (divisão de dois inteiros). Como exemplo de números irracionais, temos a raiz quadrada de 2 e a raiz quadrada de 3:

Um número irracional bastante conhecido é o número pi =3,1415926535...

· Conjunto dos números reais (IR)

Dados os conjuntos dos números racionais (Q) e dos irracionais, definimos o conjunto dos números reais como:

O diagrama abaixo mostra a relação entre os conjuntos numéricos:

Portanto, os números naturais, inteiros, racionais e irracionais são todos números reais. Como subconjuntos importantes de IR temos:

IR* = IR-{0}

IR₊ = conjunto dos números reais não negativo

IR_ = conjunto dos números reais não positivos

Obs: entre dois números inteiros existem infinitos números reais. Por exemplo:

- Entre os números 1 e 2 existem infinitos números reais:

1,01 ; 1,001 ; 1,0001 ;  1,1 ;  1,2  ; 1,5 ; 1,99 ; 1,999 ; 1,9999 ...

- Entre os números 5 e 6 existem infinitos números reais:

5,01 ; 5,02 ; 5,05 ;  5,1 ;  5,2  ; 5,5 ; 5,99 ; 5,999 ; 5,9999 ...

Atividades:

1. Num grupo de 61 pessoas 18 gostam de seriados, mas não gostam de telenovelas; 5 pessoas não gostam de telenovelas e nem de seriados; 25% das pessoas que gostam de seriados também gostam de telenovelas.
   O total de pessoas do grupo que gostam de telenovelas, mas não gostam de seriados é:
   
   
   a) 30                                   b) 32                           c) 34                                  d) 36
   
   

2. O resultado da expressão 4+16 é um número:

1. Natural
2. Inteiro
3. Racional
4. Irracional
5. N.d.a

3. Nos espaços escreva V se a afirmativa for verdadeira e F se for falsa.

1. ( ) Todo número racional é inteiro.
2. ( ) Todo número natural é racional.
3. ( ) Todas as dízimas periódicas são números irracionais.
4. ( ) O valor aproximado de Pi é 3,41.

4. A alternativa que contém a fração geratriz da dízima 2,77777... é:

1. 27/9      b) 27/99        c) 25/9      d) 25/99      e) 25/90
   
   

5. Segundo o matemático Leopold Kronecker (1823-1891), “Deus fez os números inteiros, o resto é trabalho do homem.” Os conjuntos numéricos são, como afirma o matemático, uma das grandes invenções humanas. Assim, em relação aos elementos desses conjuntos, é correto afirmar que:

1. o produto de dois números irracionais é sempre um número irracional.
2. 
   a soma de dois números irracionais é sempre um número irracional.
3. entre os números reais 3 e 4 existe apenas um número irracional.
4. entre dois números racionais distintos existe pelo menos um número racional.
5. a diferença entre dois números inteiros negativos é sempre um número inteiro negativo.

6. Qual dos números abaixo não é racional?

1. 2,53
2. 2,3333....
3. 4,189189...
4. 3,1414...
5. 2,876329736...
   
   

7. A alternativa que contém a fração geratriz da dízima 0,16666... é:
   a) 1/4     b) 1/6     c) 16/9     d) 5/3      e) 1/8
   
   

8. Um pneu de um veículo, com 40 centímetros de diâmetro, ao dar uma volta completa, percorre, aproximadamente, uma distância de: (use π = 3,14) (C = 2.π.R.)

1. 0,25 m
2. 0,50 m
3. 2,50 m
4. 5,00 m
5. 6,00 m
   
   
   DICA: Observe a transformação do centímetros para metro.

9. Uma piscina em formato circular tem diâmetro de 12 metros, se uma pessoa concluir duas voltas pela lateral da piscina, quantos metros ela terá percorrido aproximadamente? (use π = 3,14)

1. 37,68 m
2. 24 m
3. 75,36 m
4. 48 m
5. 39,53 m
   
   

10. O comitê olímpico brasileiro dispõe de uma pista circular utilizada para a prática de treinamentos e competições de ciclismo e patinação. Sabendo que essa pista tem 250 metros de comprimento, calcule o valor aproximado do raio da circunferência da pista. Utilize π = 3,14.

1. 29,8 m
2. 39,8 m
3. 23,9 m
4. 42,1 m
5. 43,3 m